Ontology
| KR Ontology |
| Lexicon |
| Top level |
| Processes |
| Causality |
| Agents |
| Relations |
| Thematic roles |
| Glossary |
| Other Links |
| KR book |
| Math & logic |
| CG standard |
| CG examples |
| Author |
| John F. Sowa |
 |
 |
Words of Wisdom
There are more things in heaven and earth, Horatio,
Than are dreamt of in your philosophy.William Shakespeare, Hamlet
The task of classifying all the words of language, or what's the same thing, all the ideas that seek expression, is the most stupendous of logical tasks. Anybody but the most accomplished logician must break down in it utterly; and even for the strongest man, it is the severest possible tax on the logical equipment and faculty.Charles Sanders Peirce, letter to editor B. E. Smith of the Century Dictionary
The art of ranking things in genera and species is of no small importance and very much assists our judgment as well as our memory. You know how much it matters in botany, not to mention animals and other substances, or again moral and notional entities as some call them. Order largely depends on it, and many good authors write in such a way that their whole account could be divided and subdivided according to a procedure related to genera and species. This helps one not merely to retain things, but also to find them. And those who have laid out all sorts of notions under certain headings or categories have done something very useful.Gottfried Wilhelm Leibniz, New Essays on Human Understanding
We must be systematic, but we should keep our systems open.Alfred North Whitehead, Modes of Thought
Definition and Scope
The subject of ontology is the study of the categories of things that exist or may exist in some domain. The product of such a study, called an ontology, is a catalog of the types of things that are assumed to exist in a domain of interest D from the perspective of a person who uses a language L for the purpose of talking about D. The types in the ontology represent the predicates, word senses, or concept and relation types of the language L when used to discuss topics in the domain D. An uninterpreted logic, such as predicate calculus, conceptual graphs, or KIF, is ontologically neutral. It imposes no constraints on the subject matter or the way the subject may be characterized. By itself, logic says nothing about anything, but the combination of logic with an ontology provides a language that can express relationships about the entities in the domain of interest.
An informal ontology may be specified by a catalog of types that are either undefined or defined only by statements in a natural language. A formal ontology is specified by a collection of names for concept and relation types organized in a partial ordering by the type-subtype relation. Formal ontologies are further distinguished by the way the subtypes are distinguished from their supertypes: an axiomatized ontology distinguishes subtypes by axioms and definitions stated in a formal language, such as logic or some computer-oriented notation that can be translated to logic; a prototype-based ontology distinguishes subtypes by a comparison with a typical member or prototype for each subtype. Large ontologies often use a mixture of definitional methods: formal axioms and definitions are used for the terms in mathematics, physics, and engineering; and prototypes are used for plants, animals, and common household items.
KR Ontology
The ontology presented on this web site is based on the book Knowledge Representation by John F. Sowa. The basic categories and distinctions have been derived from a variety of sources in logic, linguistics, philosophy, and artificial intelligence. The two most important influences have been the philosophers Charles Sanders Peirce and Alfred North Whitehead, who were pioneers in symbolic logic. Peirce was also an associate editor of the Century Dictionary, for which he wrote, revised, or edited over 16,000 definitions. In calling that task "stupendous," he was looking beyond his personal experience of writing definitions in English to the task of stating complete definitions in logic, which he said was "a labor for generations of analysts, not for one." That labor, for which there was little practical application in the 19th century, is a major challenge for the 21st. Without it, there is no hope of merging and integrating the ever expanding and multiplying databases and knowledge bases around the world.
Yet as Shakespeare observed, any philosophy is destined to be incomplete. The continuing advance of science and human experience invevitably leads to new words and ideas that require extensions to any proposed system of categories. Whitehead's motto is the best guideline for any philosopher or scientist: "We must be systematic, but we should keep our systems open."
Hierarchies of Categories
To keep the system open-ended, the KR ontology is not based on a fixed hierarchy of categories, but on a framework of distinctions, from which the hierarchy is generated automatically. For any particular application, the categories are not defined by drawing lines on a chart, but by selecting an appropriate set of distinctions. When the application-dependent distinctions are added to the basic set, a new lattice of categories can be created by pushing a button.
The icon in the upper left corner of this web page illustrates the lattice used to represent the top-level categories, but lattices can also be used to represent categories at any level. As an example of a lattice of lower-level types, Figure 1 shows beverage types classified according to the attributes alcoholic, nonalcoholic, hot, sparkling, caffeinic, madeFromGrapes, and madeFromGrain. This lattice was derived from the attributes by the method of formal concept analysis.
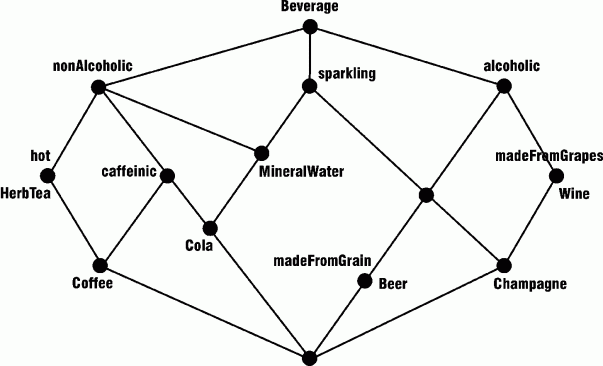
Figure 1: A lattice constructed by the method of formal concept analysis
The FCA techniques belong to the general class of data mining procedures, which find patterns in a relational database. The raw data used to generate FCA lattices is the same kind of data that could be used for other data mining techniques, such as neural networks. Each technique has its own advantages and disadvantages, depending on how the result is going to used. For ontology, the FCA technique produces a sublattice that can be automatically merged with a more general lattice of categories. In the case of Figure 1, the top node represents the type Beverage, which could be defined as DrinkableLiquid in terms of higher-level categories. For further discussion of these techniques, see the tutorial on lattices and the glossary of terminology about defining, refining, merging, and sharing ontologies.
Guide to this Web Site
The menu at the upper left of this web page lists other web pages that present the KR ontology and related background information:
- Lexicon. An article, "Concepts in the Lexicon," which is based on material taken from several published papers by John Sowa. Part I discusses the problems and issues in defining a lexicon of words in natural language and relating them to a semantic representation in logic.
- Top level. The top-level categories of the KR ontology with a discussion of the distinctions from which they were derived and the basic axioms associated with each category.
- Processes. The distinctions used to generate an ontology of process types and their relationships to verbs in natural languages and methods of reasoning about knowledge bases.
- Relations. The distinctions used to define roles and relations, including role types such as Composite, Correlative, Component, Whole, Substrate, Part, Piece, Participant, Stage, Property, Attribute, and Manner.
- Causality. Issues of causality and causation, their relation to processes and time, and their representation in logic and Petri nets.
- Agents. Linguistically, an agent is represented by the subject of an active verb. Socially, an agent is an animate being that takes responsibility for its actions in the world. Computationally, an agent is a robot or softbot that can apply general guidelines in deciding how to respond to a specific situation.
- Thematic roles. The distinctions used to define the subtypes of Participant called thematic roles, which relate concepts of verbs to the concepts of the entities that participate in the action of a verb.
- Glossary. A glossary of the terminology used for talking about ontologies and the problems and techniques for defining, refining, merging, and sharing ontologies.
- Math & logic. A 38-page tutorial of mathematical background on sets, functions, relations, graphs, lambda calculus, lattices, logic, formal grammars, and model theory.
- CG examples. Some sample sentences in English and their translation to three different, but semantically equivalent notations for logic: conceptual graphs, the Knowledge Interchange Format (KIF), and predicate calculus.
- CG standard. A web site containing the draft proposed ANSI standard for conceptual graphs and related information about CG tools.
Send comments to John F. Sowa.
Last Modified: